2021成考高起点数学预测文科2

一、选择题：本大题共17小题，每小题5分，共85分。在每小题给出的四个选项中只有一项是符合题目要求的。
1、 （　　） 
 


2、 （　　） 
 


3、函数?(x)=| x |+cosx （　　） 
A．是奇函数
B．是偶函数
C．既是奇函数也是偶函数
D．既不是奇函数也不是偶函数 


4、函数?(x)=(x²－1)3+1的最小值为（　　） 
A．?(－1)
B．?(0)
C．?(1)
D．?(2) 


5、 1位老师与6位学生站在一起拍照，要求老师站在中间，并且甲、乙两位同学要求与老师站在一起，则不同的站法种数为（　　）
 


6、 （　　） 
A．30o
B．45o
C．60o
D．75o


7、（　　） 
A．(0，3)，(0，－3)
B．(3，0)，(－3，0) 
 
A．(0，3)，(0，－3)
B．(3，0)，(－3，0) 
 


8、与圆x²+y²=4关于点M(3，2)成中心对称的曲线方程是（　　）
A．(x－3)²+(y－2)²=4
B．(x+3)²+(y+2)²=4
C．(x－6)²+(y－4)²=4
D．(x+6)²+(y+4)²=4


9、在同一坐标系中，函数y=2^－x 与y=log₂ x的图象是（　　） 
 


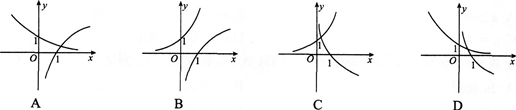
10、抛物线y²=－4x上一点P到焦点的距离为4，则它的横坐标是（　　） 
A．－4
B．－3
C．－2

D．－1

11、 不等式| 3x+1 |≤2的解集是（　　） 
 


12、已知AABC中，A：B：C=1：2：3，那么a：b：c为（　　） 
 

A．如图A
B．如图B
C．如图C
D．如图D 


13、 抛物线y²=－2x+2（　　）
A．开口向右，顶点为(－1，0)
B．开口向右，顶点为(1，0)
C．开口向左，顶点为(－1，0)
D．开口向左，顶点为(1，0)


14、 （　　） 
A．4π 
B．2π
C．π 
D．π/2 


15、 一个箱子中有100个乒乓球，其中一等品97个，二等品3个．现从中任意取出5个乒乓球，其中恰有两个二等品的抽取方法种数为（　　） 
 


16、 若不等式| x－1 |+| x－4 |A．a≤3
B．a>3
C．a>1 
D．a≤1 


17、 函数y=x²－3x+1在点M(1，－1)处的切线的斜率为（　　） 
A．0
B．－1
C．1
D．2 

二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上。
18、 函数y=x³-2x²-9x+31的驻点为________． 


19、 某学科的一次练习中，第一小组5个人成绩如下(单位：分)：98，89，70，92，90，则分数的样本方差为________．

20、 △ABC中，a，b，c分别是角A，B，C的对边．如果a²－b²－c²=bc，则角A=__________． 


21、 直线y=kx+6被圆x²+y²=25所截得的弦长为8，则实数k的值为________． 

三、解答题：本大题共4小题，共49分。解答应写出推理，演算步骤。
22、 (本小题满分12分)
用分期付款方式购买家用电器一件，价格为1150元，购买当天先付150元，以后每月这一天都交付50元，并加付欠款的利息，月利率为1％．若交付150元以后的第一个月开始算分期付款的第一个月，20个月全部付清．问分期付款的第十个月该交付多少钱?全部货款付清后，买这件家电实际花了多少钱?


23、 (本小题满分12分)
求过点A(3，2)，圆心在直线y=2x上，且与直线y=2x+5相切的圆的方程．


24、 (本小题满分12分) 
 


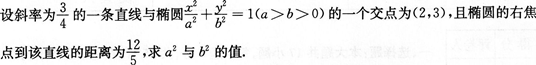
25、(本小题满分13分) 
 
(Ⅰ)求m的值； 
(Ⅱ)如果P是两曲线的一个公共点，且F₁是椭圆的另一焦点，求△PF₁F₂的面积．